▸▸▸

Multiplying Algebraic Fractions

(KS3, Year 8)

Let's start with a test!

The Test

Here is a -question, multi-choice test for the "Multiplying Algebraic Fractions" lesson. The pass mark is 90%. Don't worry! All the information you need to pass is in the lesson section under the test.

show as slides

send as homework

print as handout

This lesson is part of the algebra curriculum. According to the cookies on your browser, you haven't passed this test yet.

This test is printable and sendable

The Lesson

Algebraic fractions can be multiplied. Imagine you wanted to multiply ^a⁄_b and ^c⁄_d. a over b times c over d

How to Multiply Algebraic Fractions

To multiply algebraic fractions, use the rule: a over b times c over d equals a c over b d

A Real Example of How to Multiply Algebraic Fractions

Question

Multiply the algebraic fractions below. x over 2 times y over 3

Step-by-Step:

1

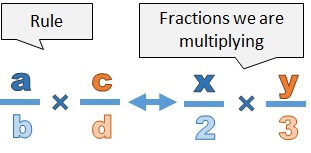Compare the fractions you are multiplying with the rule shown above. compare a over b times c over d and x over 2 times y over 3

By comparing, we see that a = x, b = 2, c = y, d = 3.

2

Use the rule, with a = x, b = 2, c = y, d = 3: a c over b d, replacing a with x, b with 2, c with y and d with 3

3

Calculate the terms in the rule. Where we have written two numbers or letters in brackets together, multiply them together:

(x)(y) = x × y = xy

(2)(3) = 2 × 3 = 6

Answer:

We have multiplied ^x⁄₂ and ^y⁄₃ together: x over 2 times y over 3 equals x y over 6

Lesson Slides

The slider below shows a real example of how to multiply algebraic fractions.

Understanding The Rule

Multiplying fractions requires:

multiplying the numerators together to form the numerator of the product...
... and multiplying the denominators together to form the denominator of the product:

This gives the rule: a over b times c times d equals a c over b d

The letters written next to each other denotes that they are multiplying each other. The rule works when the a, b, c and d are numbers, letters, terms or expressions. Make sure you can:

Multiply letters

Top Tip

Cancelling Terms

When the numerator of one fraction equals the denominator of the other fraction, they cancel each other out: $Cancel out the b that is on the top and bottom of the fraction$ This is how to simplify algebraic fractions.

This page was written by Stephen Clarke.