The Lesson
A triangle has 3 interior angles.
The interior angles of a triangle determine the type of triangle.
The interior angles of a triangle add up to 180°.Interior Angles and the Type of Triangles
Triangles are equilateral, isosceles or scalene depending on how many of the interior angles are equal to each other.
Triangles are acute, obtuse or right depending on how whether all angles are less than 90°, 1 angle is more than 90° or 1 angle is equal to 90°.
Read more about the types of triangles
The Interior Angles of a Triangle Add Up to 180°
The interior angles of any triangle add up to 180°.
The interior angles of the triangle below add up to 180°.
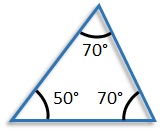
50° + 60° + 70° = 180°
How to Find a Missing Interior Angle of a Triangle
Because all the interior angles of a triangle add up to 180°, it is possible to find a missing interior angle when the two other interior angles are known. In the triangle below, we know two interior angles and want to find the third, θ.
The three interior angles must sum to 180°:
θ + 50° + 70° = 180°
By subtracting the two known angles from 180°, we find the missing angle:
θ = 180° − 50° − 70° = 60°
Read more about how to find a missing angle in a triangle
What Is a Triangle?
A triangle is a 2-dimensional shape with three sides and three angles.
)