Mathematics-Monster.com(#mm)
algebraequationsfractionspercentagesgeometrytrigonometrymore...
menu
▸▸▸

The Sum of an Interior and Exterior Angle of a Polygon Equals 180 Degrees

(KS2, Year 6)

The sum of an interior and exterior angle in a polygon is 180°:

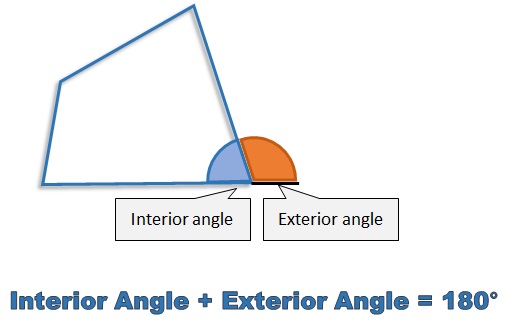sum interior exterior angle 180 degrees Don't forget: This interior angle and exterior angle must be at the same vertex (corner) of the polygon for this to be the case.

How to Find a Missing Angle Using the Sum of the Interior and Exterior Angle in a Polygon Equalling 180°

Because an interior angle and an exterior angle at a vertex sum to 180°, we can find:
  • a missing interior angle when the exterior angle is known.
  • a missing exterior angle when the interior angle is known.

Finding a Missing Interior Angle

Finding a missing interior angle is easy.

Question

What is the interior angle θ of the polygon below? sum interior exterior angle 180 degrees example 1

Step-by-Step:

1

The interior and exterior angle add up to 180°.
θ + 120° = 180°

2

Find θ by subtracting the exterior angle (120°) from 180°
θ = 180° − 120° = 60°

Answer:

The interior angle is 60°.

Finding a Missing Exterior Angle

Finding a missing exterior angle is easy.

Question

What is the exterior angle Φ of the polygon below? sum interior exterior angle 180 degrees example 2

Step-by-Step:

1

The interior and exterior angle add up to 180°.
100° + Φ = 180°

2

Find Φ by subtracting the interior angle (100°) from 180°
Φ = 180° − 100° = 80°

Answer:

The exterior angle is 80°.

Lesson Slides

The slider below shows another real example of the sum of an interior and exterior angle in a polygon equalling 180°.

Beware

Interior and Exterior Angles at the Same Vertex Add up to 180°

Only interior and exterior angles at the same vertex (corner) of the polygon add up to 180°. If they are at a different vertex, there is not necessarily any relationship between them.

sum interior exterior angle 180 degrees beware
author logo

This page was written by Stephen Clarke.

You might also like...

geometryfinding the exterior angle of a regular polygontrigonometry curriculumunderstanding right triangle

Help Us Improve Mathematics Monster

  • Do you disagree with something on this page?
  • Did you spot a typo?
Please tell us using this form.

Find Us Quicker!

  • When using a search engine (e.g., Google, Bing), you will find Mathematics Monster quicker if you add #mm to your search term.

Share This Page

share icon

If you like Mathematics Monster (or this page in particular), please link to it or share it with others.

If you do, please tell us. It helps us a lot!

Create a QR Code

create QR code

Use our handy widget to create a QR code for this page...or any page.

Worksheet

This test is printable and sendable

green heart logo