Circle Theorem: The Perpendicular Bisector of a Chord Passes Through the Center of a Circle
(KS3, Year 8)

If a line cuts through a chord of the circle, such that it crosses it at 90° and cuts it in half, that line passes through the centre of the circle.

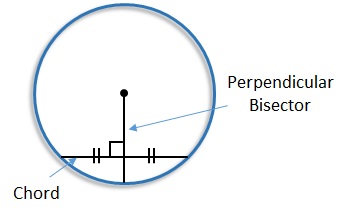
More About the Circle Theorem where the Perpendicular Bisector of a Chord Passes Through the Center of a Circle

This circle theorem deals with three properties of lines through a chord. A line that:

• is perpendicular to the chord
• bisects (cuts in half) the chord
• passes through the center of the circle.

If a line through a chord has two of these properties, it also has the third.

• A line that is perpendicular to a chord and bisects it must pass through the center of the circle.
• A line that is perpendicular to a chord and passes through the center of the circle must bisect the chord.
• A line that bisects a chord and passes through the center of a circle must be perpendicular to the chord.

Useful Definitions

A chord is a line whose endpoints lie on the circle.

The perpendicular bisector of the chord is a line that crosses the line at 90° (perpendicular) and cuts it in half (bisector).

This perpendicular bisector of the chord passes through the center of the circle.