The Lesson

The equation of a circle, with a centre with Cartesian coordinates (a, b) is in the form:

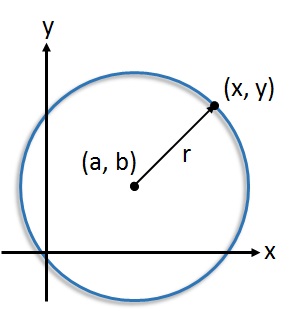
In this equation,
  • x and y are the Cartesian coordinates of points on the (boundary of the) circle.
  • a and b are the Cartesian coordinates of the centre of the circle.
  • r is the radius of the circle.
The image below shows what we mean by a point on a circle centred at (a, b) and its radius:

Real Examples of Equations of Circles (Not Centred on the Origin)

It is easier to understand the equation of a circle with examples.
  • A circle centred at (2, 3) with a radius of 5 will have the equation:

  • A circle centred at (−1, 1) with a radius of 3 will have the equation:

Lesson Slides

The slider below explains why the "Equation of a Circle" works.

Beware

The Center of a Circle Has Negative Coordinates

The equation of a circle is:

The center is (a, b).
  • The number being subtracted from the x in the brackets is the x-coordinate of the center.
  • The number being subtracted from the y in the brackets is the y-coordinate of the center.
What if a coordinate of the center is negative? Imagine the center of the circle is (−1, 2). The equation will start:
(x − −1)2 + ...
Remember, that subtracting a negative number is the same as adding the positive number:
(x − −1)2 = (x + 1)2
A negative coordinate will have a + sign in front of it. A positive coordinate will have a − sign in front of it.

Equations That Don't Quite Look Right

Don't be confused if you see an equation which looks like this:
(x − 1)2 + (y − 3)2 − 49 = 0
This is still an equation of a circle, as can be seen with a little rearranging:
(x − 1)2 + (y − 3)2 = 49

Note

Circle Centered at the Origin

A circle centered at the origin has a centre at (0, 0). If it has a radius r, the equation is:

(x − 0)2 + (y − 0)2 = r2

x2 + y2 = r2

This is the equation for a circle centered at the origin.