Mathematics-Monster.com
(#mm)

AlgebraEquationsFractionsPercentagesGeometry TrigonometryMore...
menu

Converting a Linear Equation from General to Slope-Intercept Form
(KS4, Year 10)

home▸sitemap▸linear equations▸converting a linear equation from general to slope-intercept form
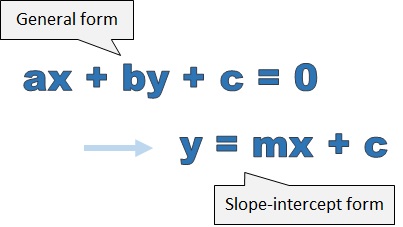
A linear equation is an equation that represents a line. We can convert a linear equation from general form to slope-intercept form. a x plus b y plus c equals 0 convert to y equals m x plus c

Why Convert from General Form to Slope-Intercept Form?

The same line can be written in general form and slope-intercept form. The two forms of linear equation tell us different things about the line.
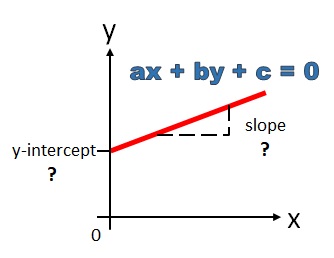
  • In general form, a, b and c do not tell us anything about the line. a x plus b y plus c equals 0 on a graph
  • In slope-intercept form, • m tells us the slope of a line • c tells us the y-intercept of a line. y equals m x plus c on a graph
If we are given a line in general form, we can convert it to slope-intercept form to understand more about the line.

How to Convert a Linear Equation from General to Slope-Intercept Form

Using algebra, we can take the general form of a linear equation and make it look like the slope intercept form.
  • Start with the linear equation in general form: a x plus b y plus c equals 0
  • Subtract ax from both sides. This has the effect of moving the ax to the other side of the equals sign (=) and changing its sign from positive to negative: b y plus c equals minus a x
  • Subtract c from both sides: b y equals minus a x minus c
  • Divide both sides by b: y equals minus a over b x minus c over b
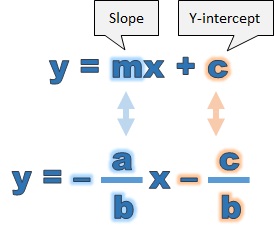
We can compare this equation with the slope-intercept form of a linear equation: Comparing a x plus b y plus c equals zero with y equals m x plus c equals zero
  • The slope is given by −a⁄b.
  • The y-intercept is given by −c⁄b.

A Real Example of How to Convert a Linear Equation from General to Slope-Intercept Form

Convert the linear equation in general form below to slope-intercept form.

Question

Find the y-intercept of the line given by the linear equation shown below. a x plus b y plus c equals 0 convert to y equals m x plus c

Step-by-Step:

1

Subtract 4x from both sides:

4x + 2y + 6 − 4x = 0 − 4x

2y + 6 = −4x

2

Subtract 6 from both sides:

2y + 6 − 6 = − 4x − 6

2y = −4x − 6

3

Divide both sides by 2:

2y ÷ 2 = (− 4x − 6) ÷ 2

y = −2x − 3

Answer:

We have converted 4x + 2y + 6 (in general form) to y = −2x − 3 (in slope-intercept form).

Lesson Slides

The slider below gives a real example of how to convert a linear equation from general form to slope-intercept form.

Interactive Widget

You can use this interactive widget to create a graph of your linear equation. Use the buttons to change the values of the linear equation.
Change the Equation
y
x
y-intercept
author logo

This page was written by Stephen Clarke.

You might also like...

linear equationsfinding the y-intercept from a linear equation in general formfinding the equation of a line between two pointsquadratic equations curriculum

Help Us Improve Mathematics Monster

  • Do you disagree with something on this page?
  • Did you spot a typo?
Please tell us using this form.

Find Us Quicker!

  • When using a search engine (e.g., Google, Bing), you will find Mathematics Monster quicker if you add #mm to your search term.

Share This Page

share icon

If you like Mathematics Monster (or this page in particular), please link to it or share it with others.

If you do, please tell us. It helps us a lot!

Create a QR Code

create QR code

Use our handy widget to create a QR code for this page...or any page.

next up:

finding the y-intercept from a linear equation in general form

Worksheet

This test is printable and sendable

green heart logo