Finding the Median from a Frequency Table
(KS2, Year 5)
How to Find the Median from a Frequency Table
Finding the median from a frequency table is easy.Question
The frequency table below shows the test scores for a class of students. What is the median test score?
Step-by-Step:
1
Make sure the entries in the Score column are in numerical order. In our example, the entries are in numerical order.
2
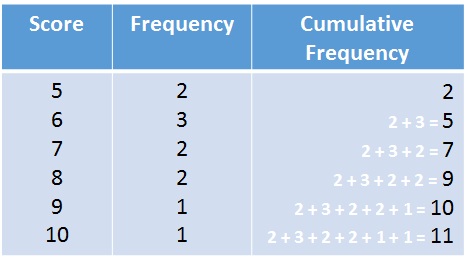
Add another column onto the table, labelled Cumulative Frequency.
For each row of the table, add the entries in the Frequency column up to that row.

3
Find the entry in the bottom row of the Cumulative Frequency column. In this example, it is 11. (Check: You should get the same result if you add up the numbers in the Frequency column).
Find the middle number of this number. (See Finding the Middle Number in the Top Tip).
In this example, there are 11 numbers, so the middle number is the 6th.
4
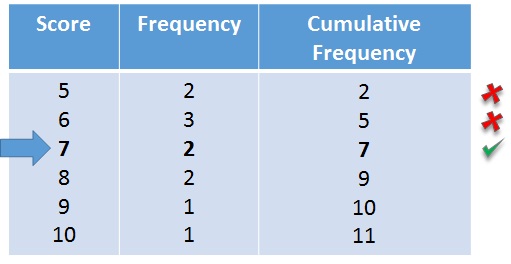
Find the first entry in the Cumulative Frequency column where this middle number (6) is first reached.
A cumulative frequency of 6 is first reached in the 3rd row.

5
Find the entry in the Score column of this row. This is the median.
Answer:
The median of the test scores is 7.
How to Find the Median from a Frequency Table (with an Even Numbered Set)
In the example above, there were 11 numbers, an odd number. (The total number of numbers is the sum of the Frequency column or the last entry in the Cumulative Frequency). The procedure is slightly different if there is an even number of numbers, which will be the case in the example below.Question
The frequency table below shows the test scores for a class of students. What is the median test score?
Step-by-Step:
1
Make sure the entries in the Scores column are in numerical order. In our example, the entries are in numerical order.
2
Add another column onto the table, labelled Cumulative Frequency.
For each row of the table, add the entries in the Frequency column up to that row.


3
Find the entry in the bottom row of the Cumulative Frequency column. In this example, it is 10. (Check: You should get the same result if you add up the numbers in the Frequency column).
Find the middle number of this number. (See Finding the Middle Number in the Top Tip).
In this example, there are 10 numbers, so the middle number is the 5.5th.
There is no 5.5th number. It is halfway between the 5th and 6th numbers. Find the 5th and 6th number.
4
Find the 5th number.
Find the first entry in the Cumulative Frequency column where 5 is first reached and read off the Score.
 A cumulative frequency of 5 is first reached in the 2nd row. This is a Score of 6. The 5th number is 6.
A cumulative frequency of 5 is first reached in the 2nd row. This is a Score of 6. The 5th number is 6.
 A cumulative frequency of 5 is first reached in the 2nd row. This is a Score of 6. The 5th number is 6.
A cumulative frequency of 5 is first reached in the 2nd row. This is a Score of 6. The 5th number is 6.
5
Find the 6th number.
Find the first entry in the Cumulative Frequency column where 6 is first reached and read off the Score.
 A cumulative frequency of 6 is first reached in the 3rd row. This is a Score of 7. The 6th number is 7.
A cumulative frequency of 6 is first reached in the 3rd row. This is a Score of 7. The 6th number is 7.
 A cumulative frequency of 6 is first reached in the 3rd row. This is a Score of 7. The 6th number is 7.
A cumulative frequency of 6 is first reached in the 3rd row. This is a Score of 7. The 6th number is 7.
6
The median is the 5.5th number, which is the mean of the 5th number (6) and the 6th number (7). Find the mean by adding the two numbers and dividing by 2.
Median = (6 + 7) ÷ 2 = 13 ÷ 2 = 6.5
Answer:
The median of the test scores is 6.5.
Interactive Widget
Here is an interactive widget to help you learn about finding the median from a frequency table.Beware
Make Sure the Numbers Are in Order
Make sure the numbers in the left most column are in order. The median is the middle number in a set of numbers that have been arranged in order. A frequency table is just a way of presenting these numbers. In the frequency table below, the numbers are not in order: The first step is to rearrange the rows so the number in the left most column are in order:
The first step is to rearrange the rows so the number in the left most column are in order: Don't forget: The whole row, not just that in the first column, needs to be rearranged. Each number in the Frequency column corresponds to the Number to its left.
Don't forget: The whole row, not just that in the first column, needs to be rearranged. Each number in the Frequency column corresponds to the Number to its left.
Note
What Is the Median?
The median is an average of a set of numbers. The median is the middle number in a set of numbers that has been arranged in order. (If there are an even number of numbers in a set, the median is the mean of the middle two numbers).Top Tip
A Formula to Find the Middle Number
The median is the middle number in an ordered set. If you know how many numbers there are in a set, which is the middle number? The formula for finding the middle number is:-
n = 11
(n + 1) ÷ 2 = (11 + 1) ÷ 2 = 6
-
n = 10
(n + 1) ÷ 2 = (10 + 1) ÷ 2 = 5.5Remember that the 5.5th number is halfway between (or the mean of) the 5th and 5th numbers.
Worksheet
This test is printable and sendable






