The Lesson
The slope of a line is its steepness. It is how far up a line goes compared to how far across it goes. The line below has a slope of 2 because it goes up 2 units for every 1 unit it goes across.
A line can be represented by a linear equation. We can find the slope from a linear equation.
Real Examples of Finding the Slope from a Linear Equation
Finding the slope of a line from a linear equation is easy. Here are some linear equations, which represent lines. We show how to find the slope from the linear equation.-
The slope of y = 2x + 1 is 2.
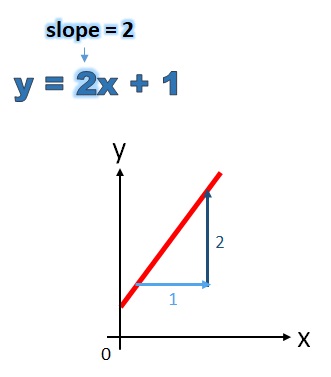Look at the number in front of the x (called the coefficient of x). This is the slope.
A slope of 2 means that the line will go up by 2 when it goes across by 1.
-
The slope of y = −3x + 3 is −3.
The number in front of the x is negative. This means the line slopes downwards.
A slope of −3 means that the line will go down by 3 when it goes across by 1.
-
y = 2 is a horizontal line. It has a slope of 0.
y = 2 does not have an x in it. We can imagine there is an invisible 0 in front of the x which gets rid of it.
A slope of 0 means that the line will neither go up nor down when it goes across by 1.
Postive And Negative Slopes
A positive slope means the line slopes up and to the right:
A negative slope means the line slopes down and to the right:
Fractional Slope
Slope can be a fraction, such as ½ and ¾. An improper fraction is positive, but less than 1. A slope of 1 gives a 45° line. A fractional slope is less steep than this:
Zero Slope And Undefined Slope
A line that goes straight across has zero slope:
A line that goes straight across has an undefined slope:
Worksheet
This test is printable and sendable
