The Lesson

The x-intercepts of a function are found where the graph of a function crosses the x-axis on a pair of Cartesian coordinate axes.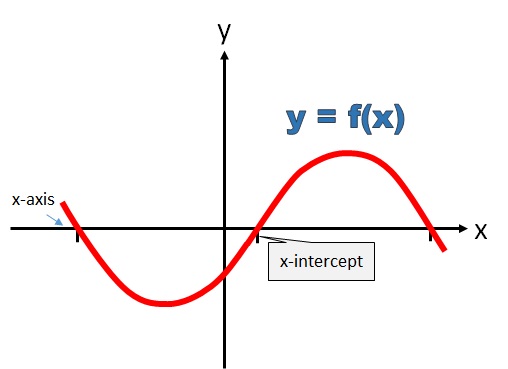

How to Find the X-intercepts of a Function

The x-intercepts of a function f(x) is found by finding the values of x which make f(x) = 0.

Write f(x) = 0, and solve for x to find the x-intercepts of a function. The method for solving for x will depend on the type of function (linear, quadratic, or trigonometric etc).

Why Does This Work?

Solving f(x) = 0 uses functional notation (see Note) to express the following idea. The function plotted on the graph is y = f(x). That is, the output of the function at each input x is assigned to y. (The input is the x-coordinate and we write the output as the y-coordinate). The x-intercepts are the ouput of the function at the x-axis. Along the x-axis, the value of y is 0. The output f(x) (which is plotted as y) of the function equals 0. The image below shows what we mean:

A Real Example of How to Find the X-intercepts of a Function

Finding the x-intercepts of a function is easy.

Question

What are the x-intercepts of the function f(x) = 2x − 4?

Step-by-Step:

1

Write the function equal to 0, f(x) = 0.
f(x) = 2x − 4 = 0

2

Find the value of x that solves the equation.

What Type of Equation Is It?

This is a linear equation.

How Do We Solve It?

Rearrange the equation to find "x = ".
2x − 4 = 0
2x − 4 + 4 = 0 + 4 Add 4 to both sides
2x = 4
2x ÷ 2 = 4 ÷ 2 Divide both sides by 2
x = 2

Answer:

The x-intercept of f(x) = 2x − 4 is 2.

Lesson Slides

The slider below shows another real example of how to find the x-intercepts of a function.

Another Real Example of How to Find the X-intercepts of a Function

Question

What are the x-intercepts of the function f(x) = x2 + 4x + 3?

Step-by-Step:

1

Write the function equal to 0, f(x) = 0.
f(x) = x2 + 4x + 3 = 0

2

Find the value of x that solves the equation.

What Type of Equation Is It?

This is a quadratic equation.

How Do We Solve It?

Factor the quadratic equation into two brackets. Set each bracket to equal 0 and find "x = ".
x2 + 4x + 3 = 0
(x + 1)(x + 3) = 0 Find two numbers that multiply to make the constant term (3) and add to the coefficient of x (4)

1 and 3 do this. Put them in brackets added to x
x + 1 = 0 ⇒ x = −1 Equate 1st bracket to 0 and solve
x + 3 = 0 ⇒ x = −3 Equate 2nd bracket to 0 and solve

Read more about how to solve quadratic equations using factoring

Answer:

The x-intercepts of f(x) = x2 + 4x + 3 are −1 and −3.

A Note on Notation

For a function, the input is often denoted by x and the function by f(x), which is equal to the output. When we plot a function on a graph, we make y = f(x). That is, the y-coordinate on the graph is equal to the output of the function.

Different Functions Are SOolved by Different Methods

Functions come in many different forms.
  • They can be linear:
  • They can be quadratic:
  • They can be trigonometic:

They are all solved by different methods. But to find the x-intercept, you always start with the same process:

How Many X-intercepts?

Different functions have different numbers of x-intercepts. Linear functions will have 1 x-intercept, unless it is a horizontal line where it will have 0 x-intercepts. Quadratic functions can have 0 or 1 or 2 x-intercepts. Trigonometric functions can have an infinite number of x-intercepts!