The Lesson

The interior angles of a polygon are the angles between two sides, inside the shape.

The Sum of the Interior Angles of a Polygon

The sum of the interior angles of a polygon is given by the formula:In this formula, n is the number of sides of the polygon. The formula tells you what the interior angles of a polygon add up to.

Example

Imagine you wanted to find the sum of the interior angles of a triangle. A triangle has 3 sides, so n = 3. Using the formula:

Sum of interior angles = (n − 2) × 180°

Sum of interior angles = (3 − 2) × 180°

Sum of interior angles = 1 × 180°

Sum of interior angles = 180°

The interior angles of a triangle add up to 180°. Read more about how to find the sum of the interior angles of a polygon

The Interior Angles of a Regular Polygon

Regular polygons have equal interior angles. There are as many interior angles as there are sides. To find each interior angle in a regular polygon, divide the sum of the interior angles by the number of sides. The formula for each of the interior angles of a regular polygon is: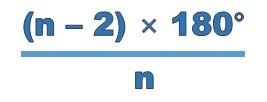

Example

Imagine you wanted to find an interior angle of a regular quadrilateral.

A square is a regular quadrilateral. It has 4 sides, so n = 4. Using the formula:

Interior angle = (n − 2) × 180° ÷ n

Interior angle = (4 − 2) × 180° ÷ 4

Interior angle = 2 × 180° ÷ 4

Interior angle = 360° ÷ 4

Interior angle = 90°

Each angle in a square is 90°. Read more about how to find the interior angle of a regular polygon

The Interior Angles of Different Polygons

Shape Sum of Interior Angles Interior Angle of Regular Polygon
Triangle 180° 60°
Quadrilateral 360° 90°
Pentagon 540° 108°
Hexagon 720° 120°
Heptagon 900° 128.57°
Octagon 1080° 135°
Nonagon 1260° 140°
Decagon 1440° 144°
Dodecagon 1800° 150°

What Is a Polygon?

A polygon is a 2-dimensional shape with straight sides.

Why Does the Formula Work?

  • The interior angles of a three-sided shape (a triangle) add up to 180°.

  • To make a four-sided shape (a quadrilateral), replace a side of the triangle with two sides. This shape is made up two triangles, and so the sum of the interior angles is 2 × 180° = 360°.

  • A five-sided shape (a pentagon) can be made by adding a third triangle, adding another 180° to the sum of the interior angles, so the sum of the interior angles is 3 × 180° = 540°.

Every time another side is added to a shape, another triangle is added, and another 180° is added to the sum of the interior angles. Note that the number of triangles is always 2 less than the number of sides. That is, there are n − 2 triangles for every n triangles. Since there are 180° for every triangle, the sum of the interior angles is (n − 2) × 180° for every n sides.

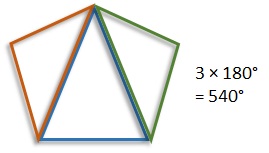
Exterior Angles

Polygons have exterior angles as well as interior angles.

The sum of the exterior angles of a polygon is 360°. Read more about the exterior angles of a polygon

An Interior and Exterior Angle in a Polygon Add Up to 180°

An interior and exterior angle in a polygon add up to 180°.

Read more about how the interior and exterior angle of a polygon add up to 180°